Wind loading represents the most critical design condition experienced by high-rise towers, light structures, large roofs and long-span bridges. For such sensitive structures, the calculation of the structural response is traditionally performed starting from data collected in wind tunnel tests. Such analyses must be able to correctly capture the dynamic response of the structure taking into consideration the stochastic nature of the wind action, the wind conditions expected on site and, when needed, effects related to fluid-structure interaction mechanisms.
If CFD is used instead of traditional wind tunnel tests it is of outmost importance that all such features, usually handled by specialised engineers in wind tunnel laboratories, are considered and accounted for by means of well established and robust procedures. In the following some analytical tools developed at LAMC and aimed at simpliyfing the calculation of the structural response to the wind action are described.
For linear buffeting analyses, the structural response to the wind action can be decomposed in a static, a quasi-static and a resonant contribution. The first one causes a static displacement related to the action of the time-averaged pressure field. The second one is related to the low frequency content of the fluctuating pressure field while the third contribution is related to the pressure fluctuations whose frequency is comparable to the natural frequencies of the considered building.
When linear dynamic analyses are performed in order to evaluate the structural response, it is important to take into consideration all possible angles of attack and ensure that simulations are sufficiently long in order to estimate the peak values of the quantities of interest. In order to perform such analyses, reduced order models of the structure are often employed.
Such models are usually built starting from the structural modes and/or influence coefficients (the effects induced on the structure by unitary normal forces statically applied in known points of the building envelope). While structural modes can be easily obtained by means of common structural solvers, the evaluation of influence coefficients is a cumbersome operation.
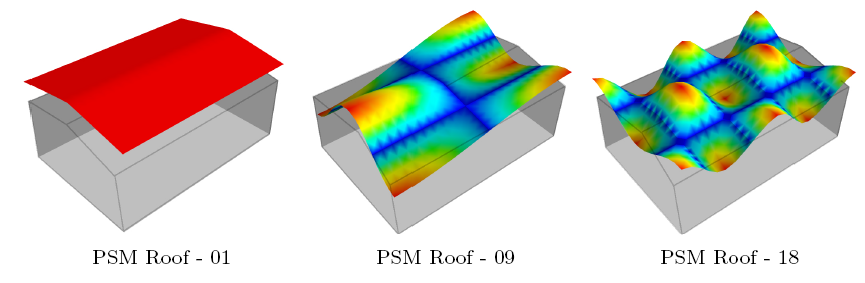
Proper Skin Modes represent an efficient alternative to traditional influence coefficients and consist in appositely built pressure distributions which depend only on the geometry of the building envelope. By adopting such an approach, the static and quasi-static behaviour of the primary structural system can be easily characterised, so allowing to efficiently build reduced order models without cumbersome manual operations. The figure reports an example of Proper Skin Modes extracted for the roof of a low-rise building.
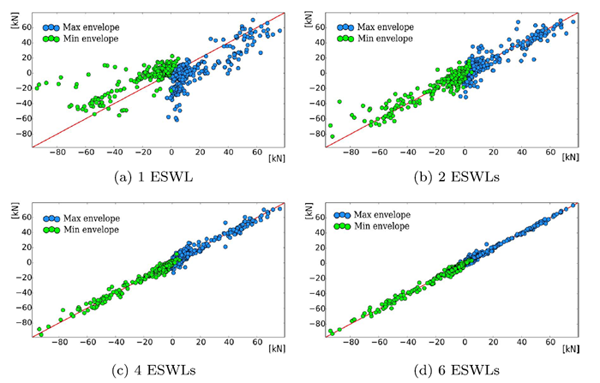
Once the structural response to the wind action has been calculated for all angles of attack, it is possible to obtain the envelope of the design values. Although such results might be directly used for design purposes, it is often convenient to search for a few load conditions which, once statically applied and enveloped together, are able to reproduce the previously obtained design values. Such operation allows to easily combine the wind action with other actions in agreement with standard design procedures.
A number of techniques have been proposed in the scientific and technical literature to this purpose. A novel efficient approach has been recently developed at LAMC which, by an appropriate smoothing of the envelope reconstruction problem, allows to efficiently calculate accurate Equivalent Static Wind Loads, ESWLs. The flexibility of the proposed procedure also allows to ensure the complete covering of the original envelope (avoiding underestimations of the applied load) and to take into account the contemporaneity between effects (e.g. axial forces and bending moments for RC sections, etc..). In the figure, the design values of the axial forces calculated for a low-rise building are reconstructed by enveloping a variable number of ESWLs. In particular, graphs report in abscissa the original envelope and in ordinate the reconstructed ones. When points are located along the bisector of the graph, a perfect matching between the original and the reconstructed envelope is obtained. It can be seen that a few ESWLs are sufficient in order to reconstruct the design envelope with good accuracy.