Page maintained by M. Iori (manuel.iori@unimore.it), V. L. de Lima (v.loti@ic.unicamp.br), S. Martello (silvano.martello@unibo.it), and M. Monaci (michele.monaci@unibo.it).
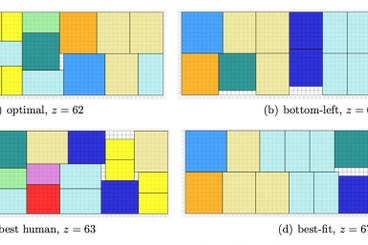
Picture taken from Costa et al. (2017)
The 2DPackLIB contains benchmarks and links for two-dimensional orthogonal cutting and packing problems.
If you need to refer to material in this library, please cite:
M. Iori, V.L. de Lima, S. Martello, M. Monaci. 2DPackLib: a two-dimensional cutting and packing library. Optimization Letters, 2021 (forthcoming).
M. Iori, V.L. de Lima, S. Martello, F.K. Miyazawa, M. Monaci. Exact solution techniques for two-dimensional cutting and packing. European Journal of Operational Research, 289(2):399–415, 2021.
Two-dimensional orthogonal cutting and packing problems
We consider two-dimensional orthogonal cutting and packing problems where both items and bins are rectangles. The four main problems in this area are:
- 2D Strip Packing Problem (2D-SPP): find a packing with minimum height;
- 2D Bin Packing Problem (2D-BPP): pack the items into the minimum number of bins;
- 2D Cutting Stock Problem (2D-CSP): a generalization of the 2D-BPP in which equivalent items are grouped into demands;
- 2D Knapsack Problem (2D-KP): find a packing of maximum value;
- 2D Orthogonal Packing Problem (2D-OPP): determine the existence of a feasible packing.
We also consider a number of variants studied in the literature, such as:
- Orthogonal Rotations;
- Guillotine Cuts;
- Variable-sized Bins;
- Loading/Unloading Constraints.
We also consider some related problems, like:
- Pallet Loading Problem;
- Continuous Berth Allocation Problem.
Surveys and typologies for two-dimensional orthogonal cutting and packing
H. Dyckhoff. A typology of cutting and packing problems. European Journal of Operational Research, 44(2):145–159, 1990.
A. Lodi, S. Martello, and D. Vigo. Recent advances on two-dimensional bin packing problems. Discrete Applied Mathematics, 123(1):379–396, 2002.
A. Lodi, S. Martello, and M. Monaci. Two-dimensional packing problems: A survey. European Journal of Operational Research, 141(2):241–252, 2002.
G. Wäscher, H. Haußner, and H. Schumann. An improved typology of cutting and packing problems. European Journal of Operational Research, 183(3):1109–1130, 2007.
N. Ntene and J.H. van Vuuren. A survey and comparison of guillotine heuristics for the 2D oriented offline strip packing problem. Discrete Optimization, 6(2):174–188, 2009.
A. Lodi, S. Martello, M. Monaci, and D. Vigo. Two-dimensional bin packing problems. In V. Th. Paschos, Paradigms of Combinatorial Optimization: Problems and New Approaches, pages 107–129, John Wiley & Sons, 2014.
E. Silva, J.F. Oliveira, and G. Wäscher. The pallet loading problem: a review of solution methods and computational experiments. International Transactions in Operational Research, 23(1-2):147–172, 2016.
J.F. Oliveira, A. Neuenfeldt Júnior, E. Silva, and M.A. Carravilla. A survey on heuristics for the two-dimensional rectangular strip packing problem>. Pesquisa Operacional, 36(2):197–226, 2016.
H. I. Christensen, A. Khan, S. Pokutta, and P. Tetali. Approximation and online algorithms for multidimensional bin packing: A survey. Computer Science Review, 24:63–79, 2017.
R. Alvarez-Valdes, M.A. Carravilla, and J.F. Oliveira. Cutting and Packing. In R. Martí, P.M. Pardalos, and M.G.C. Resende, Handbook of Heuristics, 931–977, Springer International Publishing, 2018.
M. Russo, M. Boccia, A. Sforza, and C. Sterle. Constrained two-dimensional guillotine cutting problem: upper-bound review and categorization. International Transactions in Operational Research, 27:794–834, 2020.
V.M.R. Bezerra, A.A.S. Leao, J.F. Oliveira, and M.O. Santos. Models for the two-dimensional level strip packing problem - a review and a computational evaluation. Journal of the Operational Research Society, 71(4):606–627, 2020.
Iori M., de Lima V.L., Martello S., Miyazawa F.K., Monaci M., Exact solution techniques for two-dimensional cutting and packing, European Journal of Operational Research, 289(2):399–415, 2021.
Classification according to typologies
In the following we provide the classification of the main problems according to the classical typologies:
Dyckhoff (1990) Lodi et al. (2002) Wäscher et al. (2007)
2D-SPP - 2SP|O|F ODP2D-BPP 2/V/I/M 2BP|O|F SBSBPP
2D-CSP 2/V/I/R 2BP|O|F SSSCSP
2D-KP 2/B/O 2KP|O|F SLOPP
The 2D-OPP is not classified in any typology.
The classification by Lodi et al. (2002) also covers the variants that consider orthogonal rotations (‘R’ instead of ‘O’ in the second field) and guillotine cuts (‘G’ instead of ‘F’ in the third field).
Benchmarks
We provide benchmark sets that have been used to test two-dimensional cutting and packing methods. Many of the benchmark sets have been used to test multiple 2D cutting and packing problems problems. To facilitate the test of the same set of instances on different problems, we converted the main benchmark sets for 2D cutting and packing problems with a single bin type to a standard format which comprises the four main 2D cutting and packing problems.
The instances are in the following format:
-
m
-
W H
-
for each item i (i=1,...,m)
-
index of item (i), width (wi), height (hi), demand (di), maximum number of copies (bi), profit (pi)
-
The width and height of items are part of any 2D cutting/packing problem. The demand is usually considered in the 2D-SPP, the 2D-CSP, the 2D-OPP and variants. The maximum number of copies of items is usually considered in the constrained 2D-KP and variants. The profit is considered in the 2D-KP and variants.
In the following, for each set of instances, we highlight the main problem for which the set was proposed, and the most recent papers that solved it (possibly as a different variant). The sets of instances are in 5 groups: one for each of the four main problems and an additional one for variants.
Benchmarks originally proposed for the 2D-SPP
These are the instances originally proposed for the 2D-SPP by >Hopper and Turton (2000). They were downloaded here.
The most recent results have been presented by Côté and Iori (2018) for the 2D-OPP.
These are the instances originally proposed and solved as a 2D-SPP by Hopper and Turton (2001). They were downloaded here. Some authors also refer to this class as HT.
The most recent results have been presented by Côté, Dell'Amico and Iori (2014) for the 2D-SPP, by Delorme, Iori, and Martello (2017) for the 2D-SPP with orthogonal rotations, and by Côté and Iori (2018) for the 2D-OPP.
These are the instances originally proposed and solved as a 2D-SPP by Burke, Kendall, and Whitwell (2004). They were downloaded here.
The most recent results have been presented by Côté, Dell'Amico and Iori (2014) for the 2D-SPP and by Delorme, Iori, and Martello (2017) for the 2D-SPP with orthogonal rotations.
ZDF
These are the instances originally proposed and solved as a 2D-SPP by Leung and Zhang (2011) and by Zhang et al. (2013). They were downloaded here.
Benchmarks originally proposed for the 2D-BPP and 2D-CSP
These are the instances originally proposed for the and solved as a 2D-BPP by >Bengtsson (1982). The original instances are directly presented in Bengtsson (1982).
The most recent results have been presented by Côté, Dell'Amico and Iori (2014) for the 2D-SPP and by Delorme, Iori, and Martello (2017) for the 2D-SPP with orthogonal rotations.
These are the instances originally proposed and solved as a 2D-BPP by Berkey and Wang (1987) and by Martello and Vigo (1998). They were dowloaded here.
The most recent results have been presented by Pisinger and Sigurd (2007) for the 2D-BPP, by Côté, Dell'Amico and Iori (2014) for the 2D-SPP, by Mrad (2015) as a 2D-SPP with guillotine cuts, and by Delorme, Iori, and Martello (2017) for the 2D-SPP with orthogonal rotations.
These are the instances originally proposed and solved as a 2D-CSP with guillotine cuts by Macedo, Alves, and Valério de Carvalho (2010). The instances were provided by fellow researchers.
The most recent results have been presented by Côté and Iori (2018) for the 2D-CSP with guillotine cuts and by Mrad (2015) for the 2D-SPP with guillotine cuts.
Benchmarks originally proposed for the 2D-KP
These are the instances originally proposed and solved as a 2D-KP with guillotine cuts by Christofides and Whitlock (1977). They were downloaded here. Some authors also refer to this class as ChW.
The most recent results have been presented by Velasco and Uchoa (2019) and Martin et al. (2020) for the 2D-KP with guillotine cuts, by Côté, Dell'Amico and Iori (2014) for the 2D-SPP, and by Delorme, Iori, and Martello (2017) for the 2D-SPP with orthogonal rotations.
These are the instances originally proposed and solved as a 2D-KP with guillotine cuts by Wang (1983). They were downloaded here.
The most recent results have been presented by Velasco and Uchoa (2019) for the 2D-KP with guillotine cuts.
These are the instances originally proposed and solved as a 2D-KP by Beasley (1985a). They were downloaded here.
The most recent results have been presented by Baldacci and Boschetti (2007) for the 2D-KP, by Côté, Dell'Amico and Iori (2014) for the 2D-SPP, and by Delorme, Iori, and Martello (2017) for the 2D-SPP with orthogonal rotations.
These are the instances originally proposed and solved as a 2D-KP with guillotine cuts by Beasley (1985b). They were downloaded here.
The most recent results have been presented by Martin et al. (2020)for the 2D-KP with guillotine cuts, by Côté, Dell'Amico and Iori (2014) for the 2D-SPP, by Mrad (2015) for the 2D-SPP with guillotine cuts, by Delorme, Iori, and Martello (2017) for the 2D-SPP with orthogonal rotations, and by Cintra et al (2008) for the 2D-CSP with guillotine cuts.
These are the instances originally proposed and solved as a 2D-KP with guillotine cuts by Oliveira and Ferreira (1990). They were downloaded here.
The most recent results have been presented by Velasco and Uchoa (2019) and Martin et al. (2020) for the 2D-KP with guillotine cuts.
These are the instances originally proposed and solved as 2D-KP by Fekete and Schepers (1997). The instances were provided by fellow researchers.
The most recent results have been presented by Baldacci and Boschetti (2007) for the 2D-KP and by Furini, Malaguti and Thomopulos (2016) for the 2D-KP with guillotine cuts.
These are the instances originally proposed and solved as a 2D-KP with guillotine cuts by Fayard, Hifi, and Zissimopoulos (1998). They were downloaded here.
The most recent results have been presented by Velasco and Uchoa (2019) for the 2D-KP with guillotine cuts.
These are the instances originally proposed and solved as a 2D-KP with guillotine cuts by Hifi (2001) and by Russo, Sforza, and Sterle (2014). They were downloaded here.
These are the instances originally proposed and solved as a 2D-KP with guillotine cuts by Alvarez-Valdés, Parajón, and Tamarit (2002). The instances were provided by fellow researchers.
The most recent results have been presented by Velasco and Uchoa (2019) for the 2D-KP with guillotine cuts, by Mrad (2015) for the 2D-SPP with guillotine cuts, and by Côté and Iori (2018) for the 2D-CSP with guillotine cuts.
These are the instances originally proposed and solved as a 2D-KP by Beasley (2004). They were downloaded here.
These are the instances originally proposed and solved as a 2D-KP with guillotine cuts by Morabito and Pureza (2010). They were downloaded here.
The most recent results have been presented by Velasco and Uchoa (2019) for the 2D-KP with guillotine cuts.
These are the instances originally proposed and solved as a 2D-KP with guillotine cuts by Velasco and Uchoa (2019). They were downloaded here.
Benchmarks originally proposed for the 2D-OPP
These are the instances originally proposed and solved as a 2D-OPP by Clautiaux, Jouglet, Carlier, and Moukrim. They were downloaded here.
The most recent results have been presented by Côté and Iori (2018) for the 2D-OPP.
These are the instances originally proposed and solved as a 2D-OPP by Mesyagutov, Scheithauer, and Belov (2012). They were downloaded here.
The most recent results have been presented by Côté and Iori (2018) for the 2D-OPP.
Benchmarks for other variants and related problems
For the 2D-BPP with variable-sized bins, we refer to the instances solved by Wei et al. (2013) that can be downloaded here.
For the 2D-KP with conflict graphs, we refer to the instances proposed by de Queiroz et al. (2017) that can be downloaded here.
For the 2D-OPP with unloading constraint, we refer to the instances proposed by Côté, Gendreau, and Potvin (2014) that can be donwloaded here.
For the Pallet Loading Problem, we refer to the instances proposed by Birgin, Lobato, and Morabito (2010) that can be downloaded here, and to the instances solved by Delorme, Iori, and Martello (2017) that can be downloaded here.
For the Rectangle Packing Problem, we refer to the instances solved by Delorme, Iori, and Martello(2017) that can be downloaded here.
For the Continuous Berth Allocation Problem, we refer to the instances presented in Xu and Lee (2018) that can be downloaded here.
TwoBinPack: An interactive visual tool for two-dimensional cutting and packing
An open source visual application to interactively solve rectangular cutting and packing problems can be downloaded here. For a full description of the application, see Costa et al. Instructions to use the TwoBinGame can be found in video.
Bibliography and useful links
A BibTeX file containing all the references from the survey by Iori et al. (2021) can be downloaded here.
Other links related to two-dimensional cutting and packing problems:
- ESICUP
- 2D Instance Generator by E. Silva, J.F. Oliveira, and G. Wäscher
- OR-library page of J.E. Beasley
- Cutting & Packing at Dresden University
- Pallet Loading page of E.G. Birgin R.D. Lobato, and R. Morabito
Updates
If you have suggestions or proposals to include new instances, please contact us at the e-mail addresses on the top.
References
R. Alvarez-Valdés, A. Parajón, and J. Tamarit (2002). A tabu search algorithm for large-scale guillotine (un)constrained two-dimensional cutting problems. Computers & Operations Research, 29(7):925–947.
J.E. Beasley (1985a) An exact two-dimensional non-guillotine cutting tree search procedure. Operations Research, 33(1):49–64.
J. E. Beasley (1985b). Algorithms for unconstrained two-dimensional guillotine cutting. Journal of the Operational Research Society, 36(4):297–306.
J.E. Beasley (2004). A population heuristic for constrained two-dimensional non-guillotine cutting. Discrete Optimization, 3(1):601-627.
B.-E. Bengtsson (1982). Packing rectangular pieces - a heuristic approach. The Computer Journal 25(3):353–357, 1982.
J.O. Berkey and P. Y. Wang (1987). Two dimensional finite bin packing algorithms. Journal of the Operational Research Society, 38:423–429.
E. G. Birgin, R. D. Lobato and R. Morabito (2010). An effective recursive partitioning approach for the packing of identical rectangles in a rectangle. Journal of the Operational Research Society, 61:306–320.
M. Delorme, M. Iori, and S. Martello (2017). Logic Based Benders' Decomposition for Orthogonal Stock Cutting Problem. Computers & Operations Research, 78:290–298.
E.K. Burkee, G. Kendall, and G. Whitwell (2004). A new placement heuristic for the orthogonal stock-cutting problem. Operations Research, 52(4):655–671.
F. Clautiaux, A. Jouglet, J. Carlier, and A. Moukrim (2008). A new constraint programming approach for the orthogonal packing problem. Computers & Operations Research, 35(3):944–959.
N. Christofides and C. Whitlock (1977). An algorithm for two-dimensional cutting problems. Operations Research 25(1):30–44.
G. Cintra, F. Miyazawa, Y. Wakabayashi, and E. Xavier (2008). Algorithms for two-dimensional cutting stock and strip packing problems using dynamic programming and column generation. European Journal of Operational Research, 191(1):61–85.
G. Costa, M. Delorme, M. Iori, E. Malaguti, and S. Martello (2017). A training software for orthogonal packing problems. Computers and Industrial Engineering, 11:139-147.
J.-F. Côté, M. Dell’Amico, and M. Iori (2014). Combinatorial Benders’ cuts for the strip packing problem. Operations Research, 62(3):643–661.
J.-F. Côté, M. Gendreau, and J.-Y. Potvin (2014). An exact algorithm for the two-dimensional orthogonal packing problem with unloading constraints. Operations Research, 62(5):1126–1141.
J.-F. Côté. and M. Iori (2018). The meet-in-the-middle principle for cutting and packing problems. INFORMS Journal on Computing, 30(4):646–661 .
D. Fayard, M. Hifi, and V. Zissimopoulos (1998). An efficient approach for large-scale two-dimensional guillotine cutting stock problems. Journal of the Operational Research Society, 49:1270–1277.
S.P. Fekete and J. Schepers (1997). A new exact algorithm for general orthogonal d-dimensional knapsack problems. In: R. Burkard and G. Woeginger (eds) Algorithms — ESA 1997. Lecture Notes in Computer Science, 1284. Springer, Berlin, Heidelberg.
F. Furini, E. Malaguti, and D. Thomopulos (2016).Modeling two-dimensional guillotine cutting problems via integer programming. INFORMS Journal on Computing, 28(4):736–751.
M. Hifi (2001). Exact algorithms for large-scale unconstrained two and three staged cutting problems. Computational Optimization and Applications, 18:63–88.
M. Hifi and C. Roucairol (2001). Approximate and exact algorithms for constrained (un)weighted two-dimensional two-staged cutting stock problems. Journal of Combinatorial Optimization, 5:465–494.
E. Hopper and B.C.H. Turton (2000). Problem generators for rectangular packing problems.
E. Hopper and B.C.H. Turton (2001). An empirical investigation of meta-heuristic and heuristic algorithms for a 2D packing problem. European Journal of Operational Research, 128(1):34–57.
M. Iori, V.L. de Lima, S. Martello, F.K. Miyazawa, M. Monaci (2021). Exact solution techniques for two-dimensional cutting and packing, European Journal of Operational Research, 289(2):399–415.
S.C.H. Leung, and D. Zhang (2011). A fast layer-based heuristic for non-guillotine strip packing. Expert Systems with Applications, 38(10): 13032–13042.
R. Macedo, C. Alves, and J. Valério de Carvalho (2010). Arc-flow model for the two-dimensional guillotine cutting stock problem. Computers & Operations Research 37(6):991–1001.
S. Martello and D. Vigo (1998). xact solution of the two-dimensional finite bin packing problem. Management Science, 44(3):388–399.
M. Martin, E. Birgin, R. Lobato, R. Morabito, and P. Munari (2020). Models for the two-dimensional rectangular single large placement problem with guillotine cuts and constrained pattern. International Transactions in Operational Research, 27(2):767–793.
M. Mesyagutov, G. Scheithauer, and G. Belov (2012). LP bounds in various constraint programming approaches for orthogonal packing. Computers & Operations Research, 39(10):2425–2438.
R. Morabito and V. Pureza (2010). A heuristic approach based on dynamic programming and and/or-graph search for the constrained two-dimensional guillotine cutting problem. Annals of Operations Research, 179:297–315.
M. Mrad (2015). An arc flow-based optimization approach for the two-stage guillotine strip cutting problem. Journal of the Operational Research Society, 66(11):1850-1859.
J.F. Oliveira and J.S. Ferreira (1990). An improved version of Wang’s algorithm for two-dimensional cutting problems. European Journal of Operational Research, 44:256–266.
F.G. Ortmann, N. Ntene, and J.H. van Vuuren (2010). New and improved level heuristics for the rectangular strip packing and variable-sized bin packing problems. European Journal of Operational Research, 203(2):306–315.
D. Pisinger and M. Sigurd (2005). The two-dimensional bin packing problem with variable bin sizes and costs. Discrete Optimization, 2(2):154–167.
M. Russo, A. Sforza, and C. Sterle (2014). An exact dynamic programming algorithm for large-scale unconstrained two-dimensional guillotine cutting problems. Computers & Operations Research, 50:97–114.
A.S. Velasco and E. Uchoa (2019). Improved state space relaxation for constrained two-dimensional guillotine cutting problems. European Journal of Operational Research, 272(1):106–120.
P.Y. Wang (1983). Two algorithms for constrained two-dimensional cutting stock problems. Operations Research, 31:573–586.
L. Wei, W.-C. Oon, W. Zhu, A. Lim (2013). A goal-driven approach to the 2D bin packing and variable-sized bin packing problems. European Journal of Operational Research, 224(1):110–121.
Z. Xu and C.-Y. Lee (2018). New lower bound and exact method for the continuous berth allocation problem. Operations Research, 66(3):778–798.
D. Zhang, L. Wei, S.C.H. Leung, Q. Chen (2013).A binary search heuristic algorithm based on randomized local search for the rectangular strip packing problem. INFORMS Journal on Computing, 25(2):332–345