Quantum many body systems and quantum information
The study of matter, from its fundamental constituents to its aggregate structures, is based on the understanding of the quantum effects that appear, even macroscopically, in complex many-body systems. This is the case of spin and bosonic/fermionic systems in low dimensions and at low temperature, in which new phases of matter can emerge, such as superfluidity and superconductivity or exotic states in topological materials, that are fundamental for new experimental and technological innovations with a high impact also on everyday life. Many of these models represent a paradigm for the study of systems with strong interactions, in which non-perturbative effects and quantum correlations play a crucial role, bridging the study of condensed matter systems and field theoretical models used to describe the physics of fundamental interactions of particles and gravity. In addition, the study of critical phenomena and quantum phases in complex systems is based on quantum information and computation theory, which can lead to very promising applications to data science, through the development of quantum algorithms and of new techniques such as quantum machine learning.
Research activities
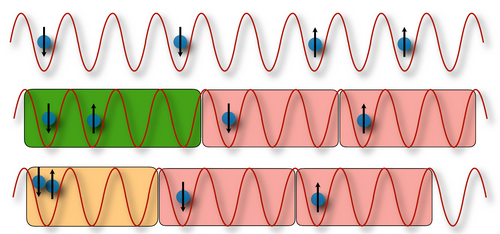
Quantum phase transitions of matter in low dimensions
The structure of the phase diagram of quantum matter in low dimensions is fixed by the properties of quantum correlations and entanglement. When combined with quantum information techniques, the use of effective field theories and of numerical algorithms (quantum Monte Carlo, Tensor Networks) allows for the study of phase transitions and the classification of phases in one-dimensional models with a vast range of both short and long range interactions, in static conditions as well as out of equilibrium. [E. Ercolessi, C. Degli Esposti Boschi, P. Pieri, L. Piroli].

Critical phenomena, integrability and entanglement
Conformal field theory and quantum integrability are very powerful tools for the study of 1+1 dimensional models that describe paradigmatic examples in condensed matter physics (e.g. the Ising model) as well as in field theory (e.g. the sine-Gordon model), by means of non-perturbative and exact techniques Both at- and out-of-equilibrium, quantum correlations and entanglement exhibit universal properties that can be calculated by means of these techniques and can be used to characterize phase transitions and quantum phases of the system. [E. Ercolessi, D. Fioravanti, L. Piroli, F. Ravanini].
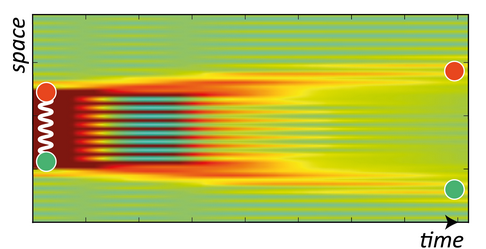
Quantum simulations of field theories
Systems of atoms/ions trapped in optical lattices yield experimental platforms in which it is possible to simulate the Hamiltonian of quantum field theories for both condensed matter and fundamental interactions in particles and gravity. By combining the theory of critical phenomena with numerical techniques which exploit the properties of quantum correlations and entanglement, such as DMRG and Tensor Networks, we study lattice field theory Hamiltonians (Schwingermodel for QED, gauge theories), by looking at non-perturbative aspects -such as confinement- or out-of-equilibrium phenomena -such as the string breaking mechanism [E. Ercolessi, P. Pieri, L. Piroli].

Quantum computation and quantum machine learning
This activity develops along two complementary lines of research. The first one is about the connections between statistical mechanics, many body theory and quantum computing, mainly in connection with the problem of quantum error correction and the characterization of physical systems, such as trapped ions, that can be used to implement quantum processors. The second deals with the possible use of classical algorithms for the study of quantum many body systems as well as that of quantum algorithms for machine learning and data analysis [E. Ercolessi, P. Pieri, L. Piroli].
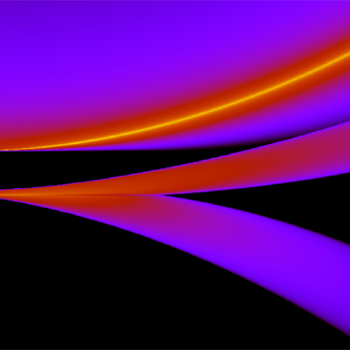
Quantum gases, superconductors, and BCS-BEC crossover
Trapped ultracold gases have recently allowed the experimental exploration of the BCS-BEC crossover (that is, the evolution that bridges the phenomenon of superconductivity to Bose-Einstein condensation), while raising at the same time several new theoretical problems. We address some of these challenges by combining many-body diagrammatic methods with the development of efficient algorithms for their numerical implementation. We use the same methods to also analyze new superconductors in condensed matter [P. Pieri].

Quantum physics - teaching and social impact
In the era of the “second quantum revolution”, it is of strategic importance to rethink how to teach quantum mechanics both at high school and university levels, keeping in mind also the impact that quantum technologies (quantum networks, quantum computers, …) will have on society. This activity is pursued in collaboration with the group of Physics Education and History of Physics of DIFA [E. Ercolessi].
National and international projects and collaborations
- QUANTUM – INFN initiative of Group IV.
- QUANTHEP - QUANTERA Project (with Instituto de Telecomunicacoes of Lisbon; University of Latvia; INFN sections of Padua and Bari).
- “Business Oriented Applications of Quantum Computations” - Project funded by "International Foundations Big data and Artificial Intelligence for Human Development" (con UNISTRA-CNRS, INFN, CINECA, LEITHÀ)
- BAT-QuO - ISCRA Project - Bayesian Adaptive Techniques for Quantum Optimization on NISQ Devices (collaboration with Cineca and PASQAL)
- CNR (Dr. Cristian Degli Esposti Boschi)
- University of Strasbourg (Prof. Guido Pupillo, Institut de Science et d’Ingénierie Supramoléculaires).
- University of Aachen (Prof. Markus Müller, Institute for Quantum information).
- University of Innsbruck (Prof. Rudolf Grimm, Institute for Experimental Physics, Center for Ultracold Atoms and Quantum gases)
- Kochi University - Japan (Dr. Hiiroyuki Tajima, Department of Natural Science)
- Università di Camerino (Prof. Giancarlo Calvanese Strinati, Prof. Andrea Perali, Dr. Sebastiano Pilati)