Quantum field theory and strings
Quantum field theory is the primary tool in theoretical physics to describe the behaviour of elementary particles and fundamental interactions. Its applicability extends also to critical phenomena in statistical mechanics and condensed matter. At the moment we have an excellent control of quantum field theory at perturbative level while a full understanding of non-perturbative effects is the subject of ongoing research. This can be achieved via approaches based on the renormalisation group, holography and dualities, supersymmetry and integrability which allow the emergence of algebraic and analytic structures that can lead to the discovery of exact results.
Another open problem of modern physics is the formulation of a consistent theory of quantum gravity and the unification of all fundamental interactions. String theory is one of the main candidates to achieve this goal and it predicts the existence of supersymmetry, extra dimensions and branes. The low-energy limit of string compactifications reproduces general relativity and Standard Model-like gauge theories. A complete understanding of the implications of string theory for particle physics and cosmology is however still missing.
Research activities
Topological and geometrical aspects of quantum field theory and strings
Non-linear sigma models. Batalin-Vilkovisky quantisation using the geometrical formulation of Alexandrov-Kontsevich-Schwartz-Zaboronsky. Higher gauge theories [R. Zucchini].
Worldline methods
Study of first quantisation techniques, known as “worldline methods”. The goal is to find new representations of scattering amplitudes and effective actions in QFT with gauge and gravitational couplings, with string inspired methods [F. Bastianelli].
Anomalies in QFT
Anomalies describe the quantum breaking of classical symmetries. They have several applications which range from constraining the matter content of gauge theories to the characterisation of non-perturbative properties of QFT and their behaviour under the action of the renormalisation group [F. Bastianelli].
QFT, CFT in d>2 and renormalisation group
The abstract space of all possible quantum field theories is characterised by points which are invariant under scale or conformal transformations (renormalisation group fixed points). Considering the symmetries determined by the spin content, we formulate new UV complete quantum field theories and study new classes of universality in statistical theories and in the construction of new models for fundamental interactions beyond the Standard Model [G.P.Vacca, L. Zambelli].
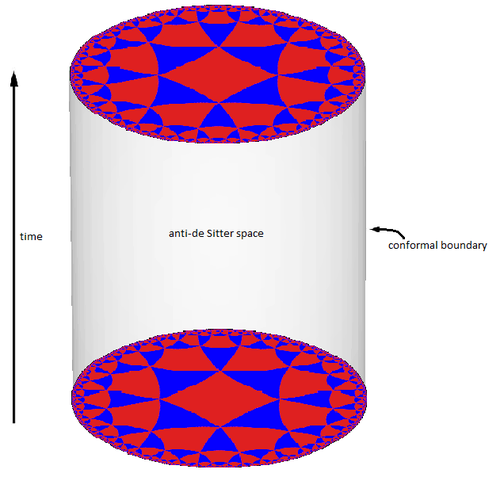
Integrability in supersymmetric theories in 4D and strings
Integrability is a fundamental property of a class of theories that allows to calculate exactly non-trivial physical properties of a given system, thanks to an underlying mathematical and physical structure. In general, this property becomes manifest in a natural way in 2D systems. In higher dimensions, it becomes then even more remarkable. Our interest is towards supersymmetric gauge theories in 4D, which also feature phenomenological applications, and their relationship with string theories, where the bidimensional structure automatically leads to integrability. Our final goal is to formulate models that are more fundamental and therefore can provide realistic description of the interactions [D. Fioravanti, D.Gregori].
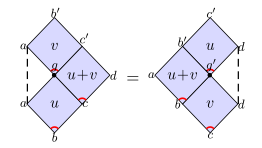
Integrability and Bethe ansatz
In integrable quantum field theories it is possible to consider, in an exact and unified way, the problems of thermodynamic behaviour and finite volume effects, using the Thermodynamic Bethe Ansatz (TBA). The development of the mathematical structures underlying TBA has revealed surprising algebraic and analytical textures, connected to other lines of research in mathematics and physics, which are under active investigation nowadays [D. Fioravanti, F. Ravanini].
Non-equilibrium physics and quantum fields
Non-equilibrium physics is one of the major challenges of modern statistical mechanics. Recent developments have highlighted the existence of QFT methods to study these phenomena, not just at classical, but also at quantum level where they are related to the physics of cold atoms and bosonic condensates. The “quantum quench” approach is now mature, while generalised hydro-dynamics (GHD) is in an active phase of recent development. Integrability and non-perturbative physics play a crucial role in both approaches. [O. Pomponio, F. Ravanini].
String compactifications
Study of the supergravity effective field theory in four dimensions for string compactifications on Calabi-Yau manifolds with branes, orientifolds and background fluxes. Derivation of perturbative and non-perturbative corrections. Stabilisation of both closed and open string moduli. Mechanisms to break supersymmetry and to realise de Sitter vacua in chiral D-brane models which are globally consistent and give rise to promising applications to cosmology and particle physics [M. Cicoli,F. Pedro].
QFT in curved spaces
Development of quantum field theory methods in curved spaces, mainly renormalisation group techniques, for applications to problems in quantum gravity and cosmology [A. Kamenchtchik].
Scattering amplitudes
Development of methods for the study and calculation of loop integrals and scattering amplitudes in quantum field theory. These rely on advanced mathematical and computational techniques such as modern methods for linear reduction, differential equations, the study of special functions, finite fields and functional reconstruction techniques. These methods can be applied to the study of a broad range of physical problems, that include interactions of the Standard Model, its extensions and gravity. [F. Bastianelli, L.De La Cruz, T.Peraro].
National and international projects and collaborations
Our research activities are also supported by the INFN initiatives ST&FI [M. Cicoli,F. Pedro], GAST [F. Bastianelli, D. Fioravanti, F. Ravanini, R. Zucchini], FLAG [A. Kamenchtchik]. Several collaborations with national (Modena, Trieste, Roma, Padova) and foreign [Morelia (MX), Potsdam (DE), Cambridge (UK), Oxford (UK), Durham (UK), King’s College (UK), City University (UK), DESY (DE), Heidelberg (DE), Perimeter (CA), Texas A&M (US), Colorado (US), Oklahoma (US), New Mexico (US), HRI Institute (IN), Ewha Seoul (KR), ENS Paris (FR), Saclay (FR), Melbourne (AU), BME Budapest (HU) ] institutions are active.