Blended structural optimization approach for WAAM beams

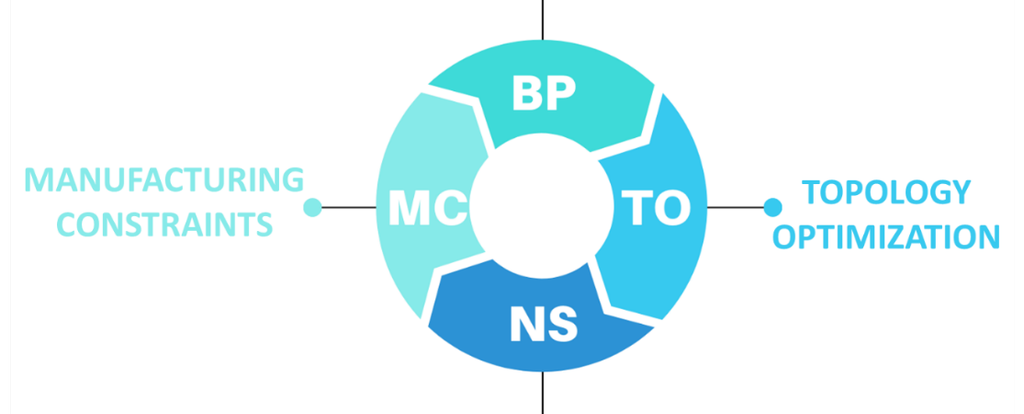
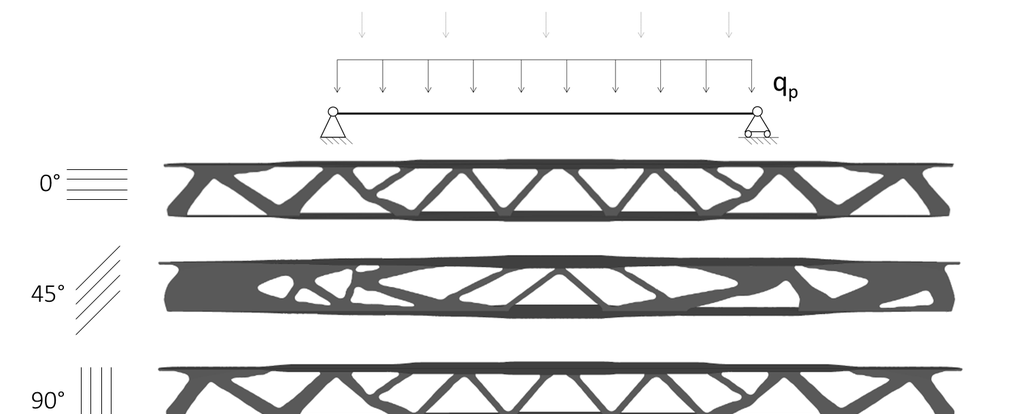
With the aim of integrating the capabilities of optimization procedures in terms of new structural shapes with the current limitations of WAAM technology (i.e. manufacturing constraints, printing precision and material properties) together with the robustness and reliability of structural design verifications, a so-called “blended” structural optimization approach is here proposed. Indeed, the approach is intended to “blend” a stiffness-based topology optimization approach (suitably tailored for WAAM stainless steel, see e.g. [43]) with basic principles of structural design in terms of conceptual design and structural solutions to conceive an initial design, together with concepts of robustness and reliability to guide the designer from the purely mathematically optimized solutions towards the final design. In fact, the optimized designs need to comply with the manufacturing constraints proper of WAAM process, and then to be structurally verified through numerical simulations using an iterative process towards the final design. This could be achieved by endowing the proposed optimization approach with multiple sets of constraints involving non-linearities, at the cost of increased complexity and computational time. A “blended” structural optimization approach may be conveniently used to investigate effective solutions in an efficient way. The fundamental aspects of the blended design approach are: the basic principles, the manufacturing constraints, the algorithms for topology optimization, the numerical simulations to verify the structural performances.

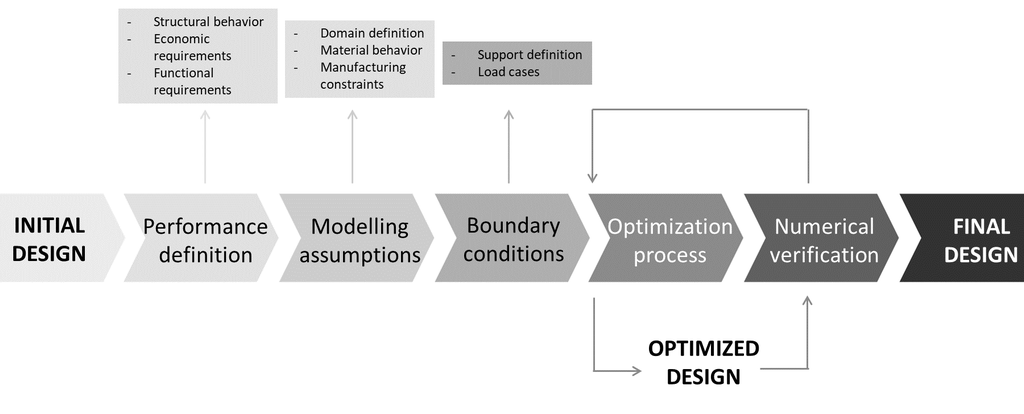
The implementation of the blended structural optimization approach can be donw through various steps. (1) First, an initial design is set based on solutions coming from the past and from basic principles of structural engineering. (2) From that, the target performances are formulated in terms of structural behavior (serviceability and ultimate limit states), economic and functional requirements (costs, aesthetics, …). (3) The definition of the modelling criteria and assumptions is set in terms of: (i) domain definition, (ii) material behavior and (iii) manufacturing constraints, such as printing angles, allowable thickness range, etc. (4) Based on the predicted application, the boundary conditions are set in terms of support definition and load cases. (5) The optimization problem is then formulated based on a subset of the data provided in (3, 4) in order to achieve the target objectives (2). This process is included in an iterative procedure in which the optimized design is first selected through a topology optimization algorithm seeking for lightweight design with prescribed stiffness, then verified in terms of its structural performances through numerical simulations. (6) Finally, the final design is selected among the optimized designs that comply with the requested structural performances (2).