Homepage

Neuromathematics

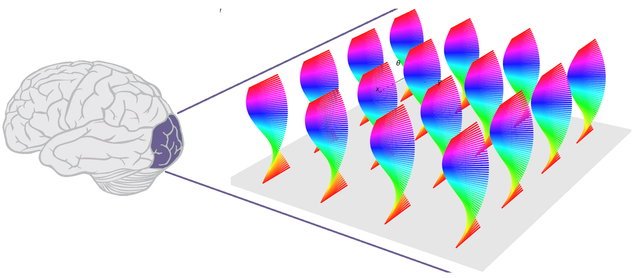
Mathematical Neuroscience involves the mathematical modeling and analysis of the nervous system, including its functions and dysfunctions. Our research group focuses on developing and applying advanced mathematical methods—drawing from sub-Riemannian geometry, contact geometry, and noncommutative harmonic analysis—to uncover the functional architectures of visual areas, the motor cortex, and their interconnections.